- Published on
KAN さわってみた
- Authors
- Name
- mount-tyo
- @mount_tyo8080
KAN さわってみた
随時,更新予定
概要
- この記事では,KAN の詳細(理論とか)については触れません.(理解していないので...)
- どんな環境を用意し,どんなコードを書けば KAN を動かすことができるのか,というタスクに対するソリューションの1つを紹介しているのみです.
- KAN の詳しい話を知りたい方は,参考のセクションに記載しているリンクが手助けになるかもしれません.
導入
最近,X で KAN という Neural Network(NN) に代わり得る新たな network を知った. なんでも,NN の学習でいうところの活性化関数を学習するとか. しかも,学習した活性化関数みたいなものを既存の関数(sinとかx^2とかexpとか)に当てはめることで,学習結果が解釈しやすいとか...
とりあえず,KAN の論文はこちら.(こちらが KAN の最初の提案論文かどうかは未調査です.)
https://arxiv.org/abs/2404.19756
ドキュメントがあったので,こちらを参考にコードを動かしてみよう.
https://kindxiaoming.github.io/pykan/index.html
KAN を試す
今回の環境は以下の感じです.
- macOS Sonoma version 14.5
- VSCode: 1.90.1
- Python: 3.10.14
$ python -V
Python 3.10.14
- Git 2.45.2
$ git -v
git version 2.45.2
手順・コードなど
# プロジェクトの dir を作成し,移動する
mkdir kan-tutorial
cd kan-tutorial
# 仮想環境を作成し,起動する
python -m venv .venv
source .venv/bin/activate
# 必要なライブラリをインストールする
pip install -U pip
pip install pykan notebook torch numpy scikit-learn matplotlib tqdm
# ipynb ファイルを作成する
touch main.ipynb
main.ipynbに以下のコードを記述する
{
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from kan import *\n",
"\n",
"# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).\n",
"model = KAN(width=[2, 5, 1], grid=5, k=3, seed=0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# create dataset f(x,y) = exp(sin(pi*x)+y^2)\n",
"f = lambda x: torch.exp(torch.sin(torch.pi * x[:, [0]]) + x[:, [1]] ** 2)\n",
"dataset = create_dataset(f, n_var=2)\n",
"dataset[\"train_input\"].shape, dataset[\"train_label\"].shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# plot KAN at initialization\n",
"model(dataset[\"train_input\"])\n",
"model.plot(beta=100)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# train the model\n",
"model.train(dataset, opt=\"LBFGS\", steps=20, lamb=0.01, lamb_entropy=10.0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model.plot()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model.prune()\n",
"model.plot(mask=True)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model = model.prune()\n",
"model(dataset[\"train_input\"])\n",
"model.plot()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model.train(dataset, opt=\"LBFGS\", steps=50)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model.plot()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"mode = \"auto\" # \"manual\"\n",
"\n",
"if mode == \"manual\":\n",
" # manual mode\n",
" model.fix_symbolic(0, 0, 0, \"sin\")\n",
" model.fix_symbolic(0, 1, 0, \"x^2\")\n",
" model.fix_symbolic(1, 0, 0, \"exp\")\n",
"elif mode == \"auto\":\n",
" # automatic mode\n",
" lib = [\"x\", \"x^2\", \"x^3\", \"x^4\", \"exp\", \"log\", \"sqrt\", \"tanh\", \"sin\", \"abs\"]\n",
" model.auto_symbolic(lib=lib)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model.symbolic_formula()[0][0]"
]
}
],
"metadata": {
"kernelspec": {
"display_name": ".venv",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.10.14"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
- VSCode で
main.ipynbを開き,コードを実行する
# VSCode を起動する
code .
# notebook で code を実行する
実行結果
学習したモデルのプロットはこちら.
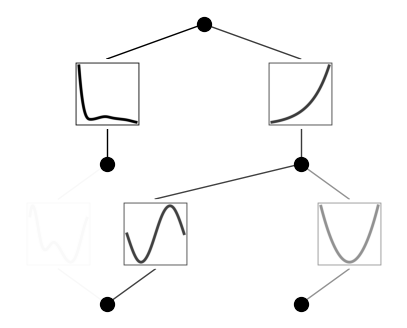
なんかドキュメントの結果とは違ったなあ... 最終的に得られた式は,
であった(数式の書き方とか Katex の書き方がよくわからんので,変でもご容赦ください...). ちょっと省略できるところは省略したり,項を移動させたりしてもう少し綺麗にすると,
とできた.作ったデータセットは,
なので, は に, は に対応していると思われる. ただ,なんか
という部分があるのが気になる. と の差分を表しているのか・・・?(調べろ,自分)
感想
今回は,このドキュメントをもとにコードを動かしてみました.
いろいろ調べる中で,KAN がざっくり何をするのかはわかった気がしますが,詳細(KAN がなぜうまく機能するか?今回動かしたコードの意味は?)はまだまだ理解が追いついていません. X でも KAN のポストをちょいちょい見かけ,GPT に KAN を組み込んだ的なものも見かけたので,もしかしたら今後,KAN が注目されていくのかもしれません. 最近の Deep Learning を支える NN の仕組みが最適であるかどうかは,まだまだ研究の余地があると思うので,引き続き追っていきたいと思います.
参考・関連リンク
いろいろな KAN の実装があるみたい?なので,見つけた github や KAN に関連しそうな論文を雑に載せておきます.
